Ôn tập Hàm số bậc nhất
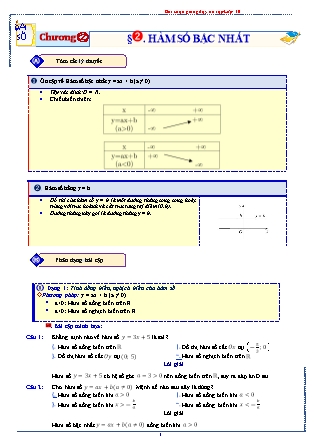
➊. Ôn tập về Hàm số bậc nhất y = ax + b (a ≠ 0)
• Tập xác định: D = R.
• Chiều biến thiên:
➋. Hàm số hằng y = b
Đồ thị của hàm số y = b là một đường thẳng song song hoặc trùng với trục hoành và cắt trục tung tại điểm (0, b).
Đường thẳng này gọi là đường thẳng y = b.
Bạn đang xem tài liệu "Ôn tập Hàm số bậc nhất", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
§➋. HÀM SỐ BẬC NHẤT
Chương ⓶
ĐẠI
SỐ
Tóm tắt lý thuyết
Ⓐ
➊. Ôn tập về Hàm số bậc nhất y = ax + b (a ≠ 0)
Tập xác định: D = R.
Chiều biến thiên:
➋. Hàm số hằng y = b
Đồ thị của hàm số y = b là một đường thẳng song song hoặc trùng với trục hoành và cắt trục tung tại điểm (0, b).
Đường thẳng này gọi là đường thẳng y = b.
Phân dạng bài tập
Ⓑ
①. Dạng 1: Tính đồng biến, nghịch biến của hàm số
²Phương pháp: y = ax + b (a ≠ 0)
a>0: Hàm số đồng biến trên R
a<0: Hàm số nghịch biến trên R
Q. Bài tập minh họa:
Khẳng định nào về hàm số y=3x+5 là sai?
{. Hàm số đồng biến trên R. |. Đồ thị hàm số cắt Ox tại -53; 0.
}. Đồ thị hàm số cắt Oy tại 0; 5. ~. Hàm số nghịch biến trên R.
Lời giải
Hàm số y=3x+5 có hệ số góc a=3>0 nên đồng biến trên R, suy ra đáp án D sai.
Cho hàm số y=ax+b(a≠0). Mệnh đề nào sau đây là đúng?
{. Hàm số đồng biến khi a>0. |. Hàm số đồng biến khi a<0.
}. Hàm số đồng biến khi x>-ba. ~. Hàm số đồng biến khi x<-ba.
Lời giải
Hàm số bậc nhất y=ax+b(a≠0) đồng biến khi a>0.
Với giá trị nào của m thì hàm số y=m-2x+5m đồng biến trên R:
{. m 2. }. m≠2. ~. m=2
Lời giải
Hàm số đồng biến khi m>2
②. Dạng 2: Xác định hàm số
²Phương pháp:
Thay tạo độ các điểm mà đồ thị đi qua để giải hệ phương trình hai ẩn số tìm a,b
Q. Bài tập minh họa:
Câu 1: Với giá trị nào của m thì hàm số y=2-mx+5m là hàm số bậc nhất
{. m 2. }. m≠2. ~. m=2
Lời giải
Điều kiện hàm số bậc nhất là 2-m≠0⇔m≠2
Câu 2. Xác định hàm số bậc nhất y=f(x) thoả mãn f(-1)=2 và f(2)=-3.
{. y=-5x+13. |. y=-x+53. }. y=-3x–1. ~. y=2x+4.
Lời giải
Câu 3. Cho hàm số y=ax+b có đồ thị đi qua hai điểm A1;1, B-2;-5. Tìm a,b.
{. a=-2;b=1 |. a=1,b=-2 }. a=2,b=-1 ~. a=-1,b=2
Lời giải
d:y=ax+b
A1;1∈dB-2;-5∈d⇔a+b=1-2a+b=-5 ⇔a=2b=-1 .
Câu 4. Với giá trị nào của a và b thì đồ thị hàm số y=ax+b đi qua các điểm A-2;1;B1;-2?
{. a=2và b=1. |. a=-1 và b=-1.
}. a=-2 và b=-1. ~. a=1và b=1.
Lời giải
Thay tọa độ các điểm A,B vào hàm số ta được hệ: -2a+b=1a+b=-2⇔a=-1b=-1.
③. Dạng 3: Nhận dạng đồ thị
²Phương pháp:
Thay tạo độ điểm mà đồ thị đi qua để xử lý tiếp bài toán
Q. Bài tập minh họa:
Câu 1: Điểm nào sau đây không thuộc đồ thị hàm số y=3x+1?
{. M2;6. |. N1;4. }. P0;1. ~. Q-1;-2.
Lời giải
Ta có 3.2+1=7≠6, do đó M2;6 không thuộc đồ thị hàm số y=3x+1.
Câu 2: Biết đồ thị hàm số y=ax+b đi qua điểm M1; 4 và có hệ số góc bằng -3. Tích P=ab?
{. P=13. |. P=21. }. P=4. ~. P=-21.
Lời giải
Vì y=ax+b có hệ số góc bằng -3 nên a=-3.
Mà y=ax+b đi qua M1; 4nên y=-3x+b⇔4=-3.1+b⇔b=7.
Do đó P=a.b=-3.7=-21.
Câu 3: Đường thẳng trong hình bên là đồ thị của một hàm số nào?
{. y=-5x+3. |. y=x+3. }. y=3-3x. ~. y=3-2x.
Lời giải
Gọi y=ax+b. Dựa vào đồ thị có 3=0.x+b0=32a+b⇔a=-2b=3.
④. Dạng 4: Bài toán tương giao
²Phương pháp:
Tìm nghiệm của phương trình hoành độ giao điểm, khai thác giả thiết xử lý bài toán
Q. Bài tập minh họa:
Câu 1. Đồ thị hàm số y=3-4x cắt trục hoành tại điểm nào sau đây
{.A43;0 . |. A0;3. }. A0;34. ~. A34;0.
Lời giải
Đồ thị hàm số cắt trục hoành : y=0⇔3-4x=0⇔x=34. Điểm A34;0.
Câu 2. Trong mặt phẳng toạ độ Oxy, cho ba đường thẳng d1:3x-4y+7=0, d2:5x+y+4=0 và d3:mx+1-my+3=0. Để ba đường thẳng này đồng quy thì giá trị của tham số m là
{. m=2. |. m=-2. }. m=0,5. ~. m=-0,5.
Lời giải
Gọi A=d1∩d2. Ta dễ dàng tìm được A-1; 1.
d1,d2 và d3đồng quy ⇒d3qua A ⇔-m+1-m+3=0⇔m=2.
Thử lại: Với m=2 thì d1:3x-4y+7=0, d2:5x+y+4=0, d3:2x-y+3=0 Vì d1,d2 và d3là ba đường thẳng phân biệt cùng đi qua điểm A nên ba đường thẳng này đồng quy.
Vậy m=2 thỏa đề bài.
Bài tập rèn luyện
Ⓒ
Với giá trị nào của thì hàm số là hàm số bậc nhất
{. . |. . }. . ~. .
Cho hàm số. Mệnh đề nào sau đây là đúng?
{. Hàm số đồng biến khi . |. Hàm số đồng biến khi .
}. Hàm số đồng biến khi . ~. Hàm số đồng biến khi .
Cho hàm số có đồ thị là đường thẳng . Khẳng định nào sau đây là khẳng định sai?
{. Hàm số đồng biến trên . |. cắt trục hoành tại điểm .
}. cắt trục tung tại điểm . ~. Hệ số góc của bằng 2.
Giá trị nào của thì hàm số nghịch biến trên tập xác định của hàm số.
{. . |. . }. . ~. .
Với những giá trị nào của thì hàm số đồng biến trên ?
{. . |. . }. . ~. .
Trong các hàm số sau, hàm số nào nghịch biến trên
{. . |. . }. . ~. .
Cho hàm số . Với giá trị nào của thì hàm số đồng biến trên ? nghịch biến trên ?
{. Với thì hàm số đồng biến trên , thì hàm số nghịch biến trên .
|. Với thì hàm số đồng biến trên , thì hàm số nghịch biến trên .
}. Với thì hàm số đồng biến trên , thì hàm số nghịch biến trên .
~. Với thì hàm số đồng biến trên , thì hàm số nghịch biến trên .
Hình vẽ sau đây là đồ thị của hàm số nào?
x
y
O
1
–2
.
{. . |. . }. . ~. .
Đồ thị hình bên biểu diễn hàm số nào sau đây?
{. . |. . }. . ~. .
Đồ thị hình bên biểu diễn hàm số nào sau đây?
{. . |. . }. . ~. .
Đồ thị hình bên biểu diễn hàm số nào sau đây?
{. . |. . }. . ~. .
Với giá trị nào của và thì đồ thị hàm số đi qua các điểm , ?
{. và . |. và .
}. và . ~. và .
Một hàm số bậc nhất có . Hỏi hàm số đó là:
{. . |. . }. . ~. .
Trong mặt phẳng Oxy cho đường thẳng (d) có phương trình . Tìm k để đường thẳng d đi qua gốc tọa độ:
{. . |. .
}. . ~. hoặc .
Phương trình đường thẳng đi qua hai điểm là:
{. . |. . }. . ~. .
Đồ thị của hàm số là hình nào?
{. |.
}. ~.
Phương trình đường thẳng đi qua một điểm và song song với trục Ox là:
{. . |. . }. . ~. .
Giá trị của m để hai đường cắt nhau tại một điểm trên trục hoành là:
{. . |. . }. . ~. .
Phương trình đường thẳng đi qua giao điểm hai đường thẳng và và song song với đường thẳng là:
{. . |. .
}. . ~. .
Đồ thị sau đây biểu diễn hàm số nào?
{. . |. . }. . ~. .
Đồ thị sau đây biểu diễn hàm số nào?
{. . |. . }. . ~. .
Cho hàm số có đồ thị là hình bên. Giá trị của a và b là:
{. và . |. và . }. và . ~. và .
Cho phương trình . Khi đó:
{. Với và thì PT đã cho là phương trình của đường thẳng song song với trục Ox.
|. Với và thì PT đã cho là phương trình của đường thẳng song song với trục Ox.
}. Với và thì PT đã cho là phương trình của đường thẳng song song với trục Ox.
~. Với và thì PT đã cho là phương trình của đường thẳng song song với Ox.
Cho hàm số . Tìm mệnh đề đúng.
{. Hàm số đồng biến trên . |. Hàm số nghịch biến trên .
}. Hàm số nghịch biến trên . ~. Hàm số đồng biến trên..
Cho hàm số . Với những giá trị nào của m thì hàm số đồng biến trên ? Nghịch biến trên ?
{. Với thì hàm số đồng biến trên ; với thì hàm số nghịch biến trên .
|. Với thì hàm số đồng biến trên ; với thì hàm số nghịch biến trên .
}. Với thì hàm số đồng biến trên ; với thì hàm số nghịch biến trên .
~. Tất cả các câu trên đều sai.
Cho hàm số . Mệnh đề nào sau đây là đúng?
{. Hàm số đồng biến khi . |. Hàm số đồng biến khi .
}. Hàm số đồng biến khi . ~. Hàm số đồng biến khi .
Có bao nhiêu giá trị nguyên của tham số thuộc đoạn để hàm số đồng biến trên
{. . |. . }. Vô số ~. .
Với những giá trị nào của m thì hàm số đồng biến?
{. . |. . }. . ~. .
Tìm để hàm số nghịch biến trên
{. . |. . }. . ~. .
Có bao nhiêu giá trị nguyên của tham số thuộc đoạn để hàm số đồng biến trên
{. . |. . }. Vô số. ~. .
Tìm giá trị thực của để hai đường thẳng và cắt nhau tại một điểm nằm trên trục tung.
{. . |. . }. . ~. .
Tìm và để đồ thị hàm số đi qua các điểm .
{. và . |. và .
}. và . ~. và
Phương trình đường thẳng đi qua hai điểm và là:
{. . |. . }. . ~. .
Đồ thị của hàm số đi qua các điểm , . Giá trị của là:
{. ; . |. ; . }. ; . ~. ; .
Tìm tất cả các giá trị thực của tham số để đường thẳng vuông góc với đường
{. . |. . }. . ~. .
Biết rằng đồ thị hàm số đi qua hai điểm và . Tính tổng .
{. . |. . }. . ~.
Cho hàm số . Tìm giá trị thực của để đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng 3.
{. . |. . }. . ~. .
Xác định đường thẳng, biết hệ số góc bằng và đường thẳng qua
{. . |. . }. . ~. .
Một hàm số bậc nhất , có và . Hàm số đó là
{. . |. . }. . ~. .
Biết rằng đồ thị hàm số đi qua điểm và vuông góc với đường thẳng . Tính tích .
{. . |. . }. . ~. .
Cho hàm số có đồ thị là đường thẳng . Đường thẳng tạo với hai trục tọa độ một tam giác có diện tích bằng:
{. . |. . }. . ~. .
Xác định để ba đường thẳng và đồng quy
{. . |. . }. . ~. .
Tìm giá trị thực của tham số để ba đường thẳng , và phân biệt và đồng qui.
{. . |. . }. . ~. .
Biết rằng đồ thị hàm số đi qua điểm và song song với đường thẳng với là gốc tọa độ và . Tính giá trị biểu thức
{. . |. . }. . ~. .
Xác định để ba đường thẳng , và đồng quy
{. . |. . }. . ~. .
Tìm phương trình đường thẳng . Biết đường thẳng đi qua điểm , cắt hai tia , và cách gốc tọa độ một khoảng bằng .
{. . |. . }. . ~. .
Hàm số được viết lại:
{. . |. .
}. . ~. .
Hàm số bằng hàm số nào sau đây?
{. . |. .
}. . ~. .
Cho hàm số . Bảng biến thiên nào sau đây là bảng biến thiên của hàm số đã cho?
{. . |. .
}. . ~. .
Đồ thị trong hình vẽ bên biểu diễn cho hàm số nào?
{. . |. . }. . ~. .
Hàm số có đồ thị là:
{. Hình 1. |. Hình 2. }. Hình 3. ~. Hình 4.
Đồ thị trong hình vẽ bên biểu diễn cho hàm số nào?
{. . |. . }. . ~. .
Đồ thị trong hình vẽ bên biểu diễn cho hàm số nào?
{. . |. . }. . ~. .
Hình vẽ sau đây là đồ thị của hàm số nào?
{. . |. . }. . ~. .
Đồ thị hình bên dưới là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
{. . |. .
}. . ~. .
BẢNG ĐÁP ÁN
1.C
2.A
3.B
4.A
5.D
6.C
7.D
8.D
9.A
10.A
11.B
12.D
13.C
14.D
15.D
16.A
17.B
18.A
19.A
20.A
21.A
22.D
23.C
24.C
25.D
26.A
27.D
28.D
29.C
30.A
31.A
32.D
33.B
34.B
35.B
36.C
37.C
38.D
39.C
40.A
41.B
42.D
43.C
44.D
45.A
46.D
47.B
48.D
49.A
50.B
51.B
52.C
53.B
54.D
55.B
Hướng dẫn giải
þ Dạng 01: Lý thuyết về hàm số bậc nhất
Câu 1. Chọn C
Điều kiện hàm số bậc nhất là .
Câu 2. Chọn A
Hàm số bậc nhất đồng biến khi .
Câu 3. Chọn B
Ta có: .
Câu 4. Chọn A
Hàm số nghịch biến trên tập xác định khi .
Câu 5. Chọn D
Hàm số đồng biến trên khi .
Câu 6. Chọn C
Hàm số có nên là hàm số nghịch biến trên .
Câu 7. Chọn D
Hàm số đồng biến trên khi .
Hàm số nghịch biến trên khi .
þ Dạng 02: Nhận dạng BBT, hàm số và đồ thị hàm số (1 công thức)
Câu 8. Chọn D
Giả sử hàm số cần tìm có dạng: .
Đồ thị hàm số đi qua hai điểm nên ta có: .
Vậy hàm số cần tìm là .
Câu 11. Chọn A
Gọi phương trình đường thẳng cần tìm là .
Vì đi qua hai điểm .
Câu 12. Chọn A
Gọi phương trình hàm số cần tìm có dạng .
Dựa vào hình vẽ, ta thấy (d) đi qua hai điểm
Câu 13. Chọn B
Phương trình đường thẳng (d) chắn trên hai trục Ox, Oy lần lượt tại hai điểm .
Suy ra phương trình đường thẳng cần tìm là
Câu 14. Chọn D
Ta có : .
Câu 15. Chọn C
Ta có
Câu 16. Chọn D
Ta có d qua
Câu 17. Chọn D
Ta có
Câu 18. Chọn A
Đồ thị của hàm số có hướng đi xuống và cắt trục tung tại điểm
Câu 19. Chọn B
Ta có mà d qua
Câu 20. Chọn A
Gọi là giao điểm của .
Ta có
Câu 21. Chọn A
Ta có Tọa độ giao điểm .
Đường thẳng
Mà d qua
Câu 22. Chọn A
Giả sử hàm số cần tìm có dạng: .
Đồ thị hàm số đi qua hai điểm nên ta có: .
Vậy hàm số cần tìm là: .
Câu 23. Chọn A
Giả sử hàm số cần tìm có dạng: .
Đồ thị hàm số đi qua hai điểm nên ta có: .
Vậy hàm số cần tìm là: .
Câu 24. Chọn D
Đồ thị hàm số đi qua hai điểm nên ta có: .
Câu 25. Chọn C
Kí hiệu và phương trình trục Ox là .
Để khi và chỉ khi
Tài liệu đính kèm:
 on_tap_ham_so_bac_nhat.docx
on_tap_ham_so_bac_nhat.docx



