Bài tập Hàm số bậc hai

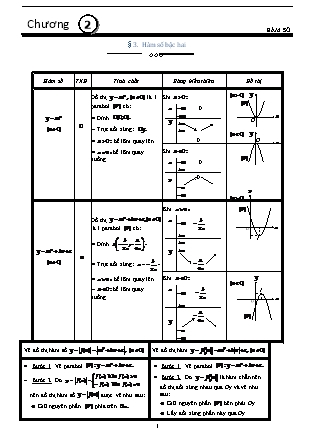
2
Chương
HÀM SỐ
§ 3. Hàm số bậc hai
¶¶¶
Hàm số
TXĐ
Tính chất
Bảng biến thiên
Đồ thị
Đồ thị là 1 parabol có:
 Đỉnh 
 Trục đối xứng: 
 bề lõm quay lên.
 bề lõm quay xuống.
Khi 
 0 
0
O
O
Khi 
 0 
0
O
I
Đồ thị là 1 parabol có:
 Đỉnh 
 Trục đối xứng: 
 bề lõm quay lên.
 bề lõm quay xuống.
 Khi 
 Khi 
O
I
Vẽ đồ thị hàm số 
Vẽ đồ thị hàm 
 Bước 1. Vẽ parabol 
 Bước 2. Do nên đồ thị hàm số được vẽ như sau:
 Giữ nguyên phần phía trên 
 Lấy đối xứng phần dưới Ox qua Ox. 
 Đồ thị là hợp 2 phần trên. 
O
 Bước 1. Vẽ parabol 
 Bước 2. Do là hàm chẵn nên đồ thị đối xứng nhau qua Oy và vẽ như sau:
 Giữ nguyên phần bên phải Oy.
 Lấy đối xứng phần này qua Oy.
 Đồ thị là hợp 2 phần trên. 
O
Tung độ đỉnh của parabol là
A. .	B. .	C. .	D. .
Lời giải
Chọn B
Ta có :Tung độ đỉnh là .
Hàm số nào sau đây có giá trị nhỏ nhất tại ?
A. .	B. .	C. .	D. .
Lời giải
Chọn D
Hàm số đạt GTNN nên loại phương án B và C.
Phương án A: Hàm số có giá trị nhỏ nhất tại nên loại.
Còn lại chọn phương án D.
Cho hàm số . Mệnh đề nào sau đây là đúng?
A. giảm trên .	B. giảm trên .
C. tăng trên .	D. tăng trên .
Lời giải
Chọn A
Ta có nên hàm số tăng trên và giảm trên nên chọn phương án A.
Hàm số nào sau đây nghịch biến trong khoảng ?
A. .	B. .	C. .	D. .
Lời giải
Chọn A
Hàm số nghịch biến trong khoảng nên loại phương án B và D. 
Phương án A: hàm số nghịch biến trên và đồng biến trên nên chọn phương án A.
Cho hàm số: . Trong các mệnh đề sau, tìm mệnh đề đúng?
A. tăng trên .	B. giảm trên .
C. Đồ thị của có đỉnh .	D. tăng trên .
Lời giải
Chọn D
Ta có nên hàm số giảm trên và tăng trên và có đỉnh nên chọn phương án D. Vì tăng trên nên tăng trên .
Bảng biến thiên của hàm số là bảng nào sau đây?
A. +∞
–∞
–∞
–∞
1
2
.	B. +∞
–∞
+∞
+∞
1
2
.
C. +∞
–∞
–∞
–∞
3
1
.	D. +∞
–∞
+∞
+∞
3
1
.
Lời giải
Chọn C
Ta có a=-2 <0 và Đỉnh của Parabol . 
Hình vẽ bên là đồ thị của hàm số nào?
1
–1
A. .	B. .	C. .	D. .
Lời giải
Chọn B
Ta có: Đỉnh và nghịch biến và .
Hình vẽ bên là đồ thị của hàm số nào?
1
–1
A. .	B. .	C. .	D. .
Lời giải
Chọn B
Ta có: Đỉnh và nghịch biến và .
Parabol đi qua hai điểm và có phương trình là:
A. .	B. .	C. .	D. . 
Lời giải
Chọn C
Ta có: Vì .
Parabol đi qua và có đỉnh có phương trình là:
A. .	B. .
C. .	D. .
Lời giải
Chọn D
Parabol có đỉnh nên ta có : 	(1)
Parabol đi qua nên ta có : 	(2)
Từ (1) và (2) ta có : .
Vậy phương trình parabol cần tìm là : .
Parabol đạt cực tiểu bằng tại và đi qua có phương trình là:
A. .	B. .	C. .	D. .
Lời giải
Chọn A
Ta có: .(1)
Mặt khác : Vì (2)
Kết hợp (1),(2) ta có : .Vậy .
Parabol đi qua ,,có phương trình là:
A. .	B. .	C. .	D. . 
Lời giải
Chọn B
Ta có: Vì .
Vậy .
Cho : và . Để ngắn nhất thì:
A. .	B. .	C. .	D. .
Lời giải
Chọn A
Gọi (loại đáp án C, D)
Mặt khác: 
(thế từ hai đáp án còn lại vào nhận được với sẽ nhận được ngắn nhất).
Giao điểm của parabol : với trục hoành:
A. ; .	B. . 	C. ;.	D. .
Lời giải
Chọn A
Cho .
Giao điểm của parabol (P): với đường thẳng là:
A. ; .	B. ;.	C. ;.	D. ;.
Lời giải
Chọn A
Cho .
Giá trị nào của thì đồ thị hàm số cắt trục hoành tại hai điểm phân biệt?
A. .	B. .	C. .	D. .
Lời giải
Chọn D
Cho (1)
Để đồ thị cắt trục hoành tại hai điểm phân biệt khi phương trình (1) có hai nghiệm phân biệt
 .
Khi tịnh tiến parabol sang trái 3 đơn vị, ta được đồ thị của hàm số:
A. .	B. 	C. .	D. .
Lời giải
Chọn A
Đặt ta có .
Cho hàm số . Đồ thị hàm số này có thể được suy ra từ đồ thị hàm số bằng cách
A. Tịnh tiến parabol sang trái đơn vị, rồi lên trên đơn vị.
B. Tịnh tiến parabol sang phải đơn vị, rồi lên trên đơn vị.
C. Tịnh tiến parabol sang trái đơn vị, rồi xuống dưới đơn vị.
D. Tịnh tiến parabol sang phải đơn vị, rồi xuống dưới đơn vị.
Lời giải
Chọn A
Ta có 
Vậy nên ta chọn đáp án A.
Nếu hàm số có và thì đồ thị của nó có dạng:
A. x
y
O
	B. x
y
O
	C. x
y
O
	D. x
y
O
Lời giải
Chọn D
Vì Loại đáp án A,B.
 chọn đáp án D.
x
y
O
Nếu hàm số có đồ thị như sau thì dấu các hệ số của nó là: 
A. 	B. 
C. 	D. 
Lời giải
Chọn B
Nhận xét đồ thị hướng lên nên .
Giao với tại điểm nằm phí dưới trục hoành nên .
Mặt khác Vì và Đỉnh I nằm bên trái trục hoành nên .
Cho phương trình: . Với giá trị nào của và thì phương trình đã cho là đường thẳng song song với trục ?
A. 	B. 
C. 	D. 
Lời giải
Chọn C
Ta có: 
Muốn song song với thì có dạng 
Nên .
Cho hàm số f . Khi đó:
A. tăng trên khoảng và giảm trên khoảng .
B. giảm trên khoảng và tăng trên khoảng .
C. luôn tăng.	
D. luôn giảm.
Lời giải
Chọn B
Ta có và 
Vậy hàm số giảm trên khoảng và tăng trên khoảng 
Cho hàm số . Trong các mệnh đề sau đây, tìm mệnh đề đúng?
A. tăng trên khoảng .	B. giảm trên khoảng 	
C. Đồ thị của có đỉnh 	D. tăng trên khoảng
Lời giải
Chọn D
Ta có và 
Vậy hàm số giảm trên khoảng và tăng trên khoảng .
Hàm số . Khi đó:
A. Hàm số đồng biến trên và nghịch biến trên 	
B. Hàm số nghịch biến trên và đồng biến trên 	
C. Hàm số đồng biến trên và nghịch biến trên 	
D. Hàm số nghịch biến trên và đồng biến trên 
Lời giải
Chọn D
Ta có và 
Vậy hàm số giảm trên khoảng và tăng trên khoảng .
Cho hàm số . Khi đó:
A. Hàm số tăng trên khoảng 	B. Hàm số giảm trên khoảng 	
C. Hàm số tăng trên khoảng 	D. Hàm số giảm trên khoảng 
Lời giải
Chọn D
Ta có và 
Vậy hàm số giảm trên khoảng và tăng trên khoảng .
Cho hàm số . Trong các mệnh đề sau mệnh đề nào đúng?
A. Hàm số luôn luôn tăng.	
B. Hàm số luôn luôn giảm.
C. Hàm số giảm trên khoảng và tăng trên khoảng 
D. Hàm số tăng trên khoảng và giảm trên khoảng 
Lời giải
Chọn C
Ta có và 
Vậy hàm số giảm trên khoảng và tăng trên khoảng .
Cho hàm số . Trong các mệnh đề sau mệnh đề nào sai?
A. giảm trên khoảng 	B. tăng trên khoảng 
C. giảm trên khoảng 	D. tăng trên khoảng.
Lời giải
Chọn D
Ta có và .
Vậy hàm số tăng trên khoảng và giảm trên khoảng .
Cho parabol . Khẳng định đúng nhất trong các khẳng định sau là:
A. có đỉnh 	B. có trục đối xứng 
C. cắt trục tung tại điểm 	D. Cả , đều đúng. 
Lời giải
Chọn D
Ta có và 
 là trục đố xứng.
 hàm số tăng trên khoảng và giảm trên khoảng .
Cắt trục .
Đường thẳng nào trong các đường thẳng sau đây là trục đối xứng của parabol ?
A. .	B. .	C. .	D. .
Lời giải
Chọn C
Ta có và .
Vậy là trục đối xứng.
Đỉnh của parabol nằm trên đường thẳng nếu bằng
A. 2. 	B. .	C. .	D. . 
Lời giải
Chọn D
Ta có: 
Để nên .
Parabol 
A. Có đỉnh.	B. Có đỉnh.
C. Có đỉnh.	D. Đi qua điểm .
Lời giải
Chọn C
Đỉnh parabol .
(thay hoành độ đỉnh vào phương trình parabol tìm tung độ đỉnh).
Cho Parabol và đường thẳng. Khi đó:
A. Parabol cắt đường thẳng tại hai điểm phân biệt.
B. Parabol cắt đường thẳng tại điểm duy nhất.
C. Parabol không cắt đường thẳng.
D. Parabol tiếp xúc với đường thẳng có tiếp điểm là.
Lời giải
Chọn A
Phương trình hoành độ giao điểm của 2 đường là:
Vậy parabol cắt đường thẳng tại hai điểm phân biệt.
Parabol . Khi đó
A. Có trục đối xứng và đi qua điểm .
B. Có trục đối xứng và đi qua điểm .
C. Có trục đối xứng và đi qua điểm .
D. Có trục đối xứng và đi qua điểm .
Lời giải
Chọn C
Trục đối xứng 
Ta có .
Cho parabol biết rằng parabol đó cắt trục hoành tại và . Parabol đó là:
A. .	B..	C..	D. .
Lời giải
Chọn D
Parabol cắt Ox tại .
Khi đó 
Vậy .
Cho parabol biết rằng parabol đó đi qua hai điểm và . Parabol đó là
A. .	B. . 	C. .	D. .
Lời giải
Chọn C
.
Vậy .
Cho parabol biết rằng parabol đó đi qua hai điểm và. Parabol đó là
A. .	B. .	C. .	D. .
Lời giải
Chọn D
.
Vậy .
Biết parabol đi qua gốc tọa độ và có đỉnh. Giá trị a, b, c là
A. . 	B. . 
C. .	D. .
Lời giải
Chọn B
Parabol qua gốc tọa độ O
Parabol có đỉnh .